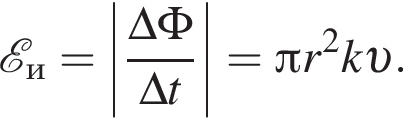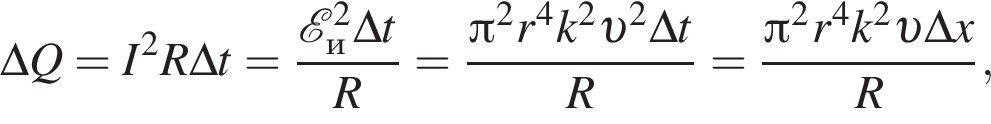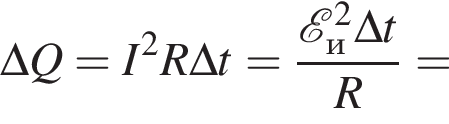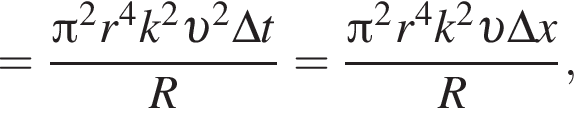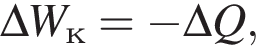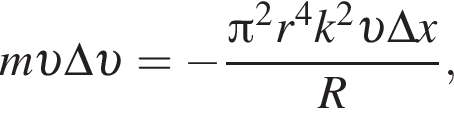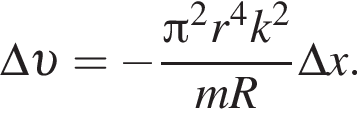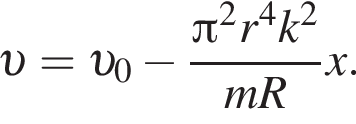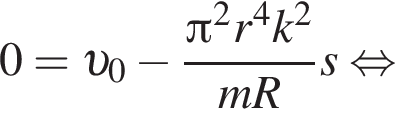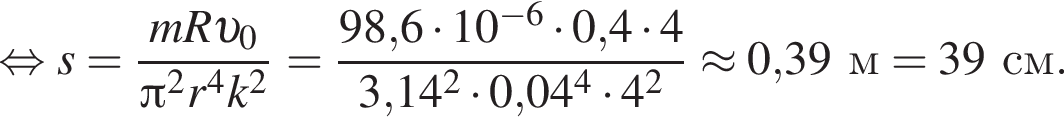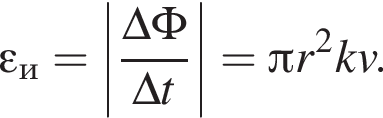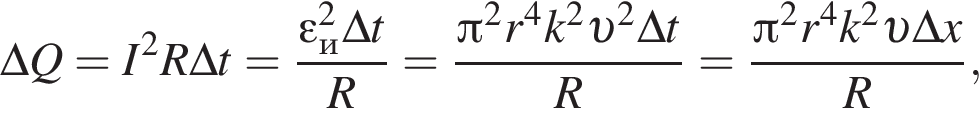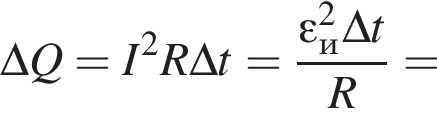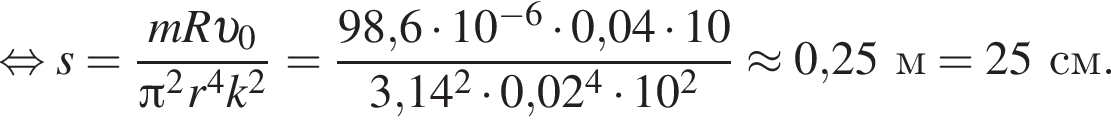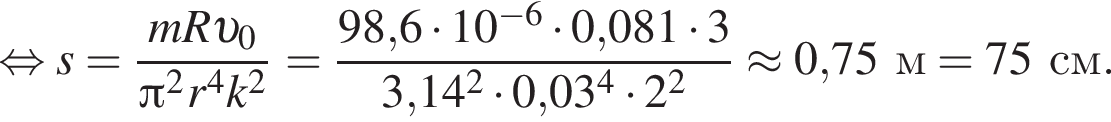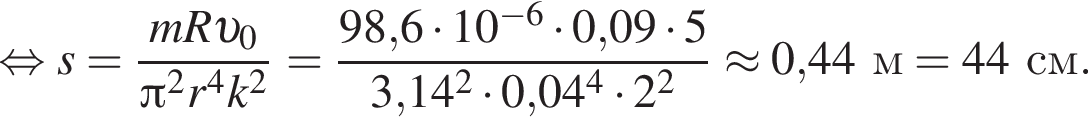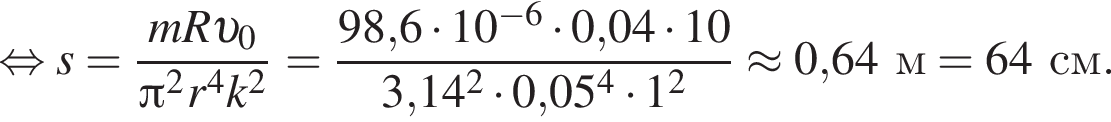Два тонких проводящих контура, силы тока в которых І1 и І2, расположены в одной плоскости (см. рис.). Если в точке О (в центре обоих контуров) модули индукции магнитных полей, создаваемых каждым из токов, B1 = 6,0 мТл и B2 = 8,0 мТл, то модуль индукции B результирующего магнитного поля в точке О равен:
По двум длинным прямолинейным проводникам, перпендикулярным плоскости рисунка, протекают токи, создающие в точке A магнитное поле (см.рис.). Сила тока в проводниках одинакова. Если в точку A поместить магнитную стрелку, то ее ориентация будет такая же, как и у стрелки под номером:
Два тонких проводящих контура, силы тока в которых I1 и I2, расположены в одной плоскости (см. рис.). Если в точке O (в центре обоих контуров) модули индукции магнитных полей, создаваемых каждым из токов, B1 =3,0 мТл и B2 =4,0 мТл, то модуль индукции B результирующего магнитного поля в точке O равен:
Два тонких проводящих контура, силы тока в которых I1 и I2, расположены в одной плоскости (см. рис.). Если в точке O (в центре обоих контуров) модули индукции магнитных полей, создаваемых каждым из токов, B1 = 10,0 мТл и B2 = 6,0 мТл, то модуль индукции B результирующего магнитного поля в точке O равен:
По двум длинным прямолинейным проводникам, перпендикулярным плоскости рисунка, протекают токи, создающие в точке A магнитное поле (см.рис.). Сила тока в проводниках одинакова. Если в точку A поместить магнитную стрелку, то ее ориентация будет такая же, как и у стрелки под номером:
Два тонких проводящих контура, силы тока в которых I1 и I2, расположены в одной плоскости (см. рис.). Если в точке O (в центре обоих контуров) модули индукции магнитных полей, создаваемых каждым из токов, B1 = 7,0 мТл и B2 = 8,0 мТл, то модуль индукции B результирующего магнитного поля в точке O равен:
По двум длинным прямолинейным проводникам, перпендикулярным плоскости рисунка, протекают токи, создающие в точке A магнитное поле (см.рис.). Сила тока в проводниках одинакова. Если в точку A поместить магнитную стрелку, то ее ориентация будет такая же, как и у стрелки под номером:
Два тонких проводящих контура, силы тока в которых I1 и I2, расположены в одной плоскости (см. рис.). Если в точке O (в центре обоих контуров) модули индукции магнитных полей, создаваемых каждым из токов, B1 = 6,0 мТл и B2 = 8,0 мТл, то модуль индукции B результирующего магнитного поля в точке O равен:
Два тонких проводящих контура, силы тока в которых I1 и I2, расположены в одной плоскости (см. рис.). Если в точке O (в центре обоих контуров) модули индукции магнитных полей, создаваемых каждым из токов, B1 = 6,0 мТл и B2 = 9,0 мТл, то модуль индукции B результирующего магнитного поля в точке O равен:
По двум длинным прямолинейным проводникам, перпендикулярным плоскости рисунка, протекают токи, создающие в точке A магнитное поле (см.рис.). Сила тока в проводниках одинакова. Если в точку A поместить магнитную стрелку, то ее ориентация будет такая же, как и у стрелки под номером:
Два тонких проводящих контура, силы тока в которых I1 и I2, расположены в одной плоскости (см. рис.). Если в точке O (в центре обоих контуров) модули индукции магнитных полей, создаваемых каждым из токов, B1 = 10,0 мТл и B2 = 8,0 мТл, то модуль индукции B результирующего магнитного поля в точке O равен:
По двум длинным прямолинейным проводникам, перпендикулярным плоскости рисунка, протекают токи, создающие в точке A магнитное поле (см.рис.). Сила тока в проводниках одинакова. Если в точку A поместить магнитную стрелку, то ее ориентация будет такая же, как и у стрелки под номером:
Прямой проводник с током I расположен перпендикулярно плоскости рисунка (см.рис. 1). В точку А поместили небольшую магнитную стрелку, которая может поворачиваться вокруг вертикальной оси, перпендикулярной плоскости рисунка. Как расположится стрелка? Правильный ответ на рисунке 2 обозначен цифрой:
поле не создается, ориентация стрелки будет произвольная
Прямой проводник с током I расположен перпендикулярно плоскости рисунка (см.рис. 1). В точку А поместили небольшую магнитную стрелку, которая может поворачиваться вокруг вертикальной оси, перпендикулярной плоскости рисунка. Как расположится стрелка? Правильный ответ на рисунке 2 обозначен цифрой:
поле не создается, ориентация стрелки будет произвольная
Четыре длинных прямолинейных проводника, сила тока в которых одинакова, расположены в воздухе параллельно друг другу так, что центры их поперечных сечений находятся в вершинах квадрата (см. рис. 1). Направление вектора индукции ![]() результирующего магнитного поля, созданного этими токами в точке O, на рисунке 2 обозначено цифрой:
результирующего магнитного поля, созданного этими токами в точке O, на рисунке 2 обозначено цифрой:
Четыре длинных прямолинейных проводника, сила тока в которых одинакова, расположены в воздухе параллельно друг другу так, что центры их поперечных сечений находятся в вершинах квадрата (см.рис. 1). Направление вектора индукции ![]() результирующего магнитного поля, созданного этими токами в точке O, на рисунке 2 обозначено цифрой:
результирующего магнитного поля, созданного этими токами в точке O, на рисунке 2 обозначено цифрой:
Прямой проводник с током I расположен перпендикулярно плоскости рисунка (см.рис. 1). В точку А поместили небольшую магнитную стрелку, которая может поворачиваться вокруг вертикальной оси, перпендикулярной плоскости рисунка. Как расположится стрелка? Правильный ответ на рисунке 2 обозначен цифрой:
поле не создается, ориентация стрелки будет произвольная
В магнитном поле, линии индукции
![]() которого изображены на рисунке, помещены небольшие магнитные стрелки, которые могут свободно вращаться. Южный полюс стрелки на рисунке светлый, северный — темный. В устойчивом положении находится стрелка, номер которой:
которого изображены на рисунке, помещены небольшие магнитные стрелки, которые могут свободно вращаться. Южный полюс стрелки на рисунке светлый, северный — темный. В устойчивом положении находится стрелка, номер которой:
Прямой проводник с током I расположен перпендикулярно плоскости рисунка (см.рис. 1). В точку А поместили небольшую магнитную стрелку, которая может поворачиваться вокруг вертикальной оси, перпендикулярной плоскости рисунка. Как расположится стрелка? Правильный ответ на рисунке 2 обозначен цифрой:
поле не создается, ориентация стрелки будет произвольная
Четыре длинных прямолинейных проводника, сила тока в которых одинакова, расположены в воздухе параллельно друг другу так, что центры их поперечных сечений находятся в вершинах квадрата (см.рис. 1). Направление вектора индукции ![]() результирующего магнитного поля, созданного этими токами в точке O, на рисунке 2 обозначено цифрой:
результирующего магнитного поля, созданного этими токами в точке O, на рисунке 2 обозначено цифрой:
Прямой проводник с током I расположен перпендикулярно плоскости рисунка (см.рис. 1). В точку А поместили небольшую магнитную стрелку, которая может поворачиваться вокруг вертикальной оси, перпендикулярной плоскости рисунка. Как расположится стрелка? Правильный ответ на рисунке 2 обозначен цифрой:
поле не создается, ориентация стрелки будет произвольная
Четыре длинных прямолинейных проводника, сила тока в которых одинакова, расположены в воздухе параллельно друг другу так, что центры их поперечных сечений находятся в вершинах квадрата (см.рис. 1). Направление вектора индукции ![]() результирующего магнитного поля, созданного этими токами в точке O, на рисунке 2 обозначено цифрой:
результирующего магнитного поля, созданного этими токами в точке O, на рисунке 2 обозначено цифрой:
Четыре длинных прямолинейных проводника, сила тока в которых одинакова, расположены в воздухе параллельно друг другу так, что центры их поперечных сечений находятся в вершинах квадрата (см.рис. 1). Направление вектора индукции ![]() результирующего магнитного поля, созданного этими токами в точке O, на рисунке 2 обозначено цифрой:
результирующего магнитного поля, созданного этими токами в точке O, на рисунке 2 обозначено цифрой:
В магнитном поле, линии индукции
![]() которого изображены на рисунке, помещены небольшие магнитные стрелки, которые могут свободно вращаться. Южный полюс стрелки на рисунке светлый, северный — темный. В устойчивом положении находится стрелка, номер которой:
которого изображены на рисунке, помещены небольшие магнитные стрелки, которые могут свободно вращаться. Южный полюс стрелки на рисунке светлый, северный — темный. В устойчивом положении находится стрелка, номер которой:
В магнитном поле, линии индукции
![]() которого изображены на рисунке, помещены небольшие магнитные стрелки, которые могут свободно вращаться. Южный полюс стрелки на рисунке светлый, северный — темный. В устойчивом положении находится стрелка, номер которой:
которого изображены на рисунке, помещены небольшие магнитные стрелки, которые могут свободно вращаться. Южный полюс стрелки на рисунке светлый, северный — темный. В устойчивом положении находится стрелка, номер которой:
В магнитное поле, линии индукции
![]() которого изображены на рисунке, помещены небольшие магнитные стрелки, которые могут свободно вращаться. Южный полюс стрелки на рисунке светлый, северный — темный. В устойчивом положении находится стрелка, номер которой:
которого изображены на рисунке, помещены небольшие магнитные стрелки, которые могут свободно вращаться. Южный полюс стрелки на рисунке светлый, северный — темный. В устойчивом положении находится стрелка, номер которой:
В магнитное поле, линии индукции
![]() которого изображены на рисунке, помещены небольшие магнитные стрелки, которые могут свободно вращаться. Южный полюс стрелки на рисунке светлый, северный — темный. В устойчивом положении находится стрелка, номер которой:
которого изображены на рисунке, помещены небольшие магнитные стрелки, которые могут свободно вращаться. Южный полюс стрелки на рисунке светлый, северный — темный. В устойчивом положении находится стрелка, номер которой:
Два длинных тонких прямолинейных проводника, сила тока в которых одинакова, расположены в воздухе параллельно друг другу так, что центры их поперечных сечений находятся в вершинах прямоугольного равнобедренного треугольника (см. рис. 1). Направление вектора индукции В результирующего магнитного поля, созданного этими токами в точке О, на рисунке 2 обозначено цифрой:
Три длинных тонких прямолинейных проводника, сила тока в которых одинакова, расположены в воздухе параллельно друг другу так, что центры их поперечных сечений находятся в вершинах прямоугольного равностороннего треугольника (см. рис. 1). Направление вектора индукции ![]() результирующего магнитного поля, созданного этими токами в точке О, на рисунке 2 обозначено цифрой:
результирующего магнитного поля, созданного этими токами в точке О, на рисунке 2 обозначено цифрой:
Два длинных тонких прямолинейных проводника, сила тока в которых одинакова, расположены в воздухе параллельно друг другу так, что центры их поперечных сечений находятся в вершинах прямоугольного равнобедренного треугольника (см. рис. 1). Направление вектора индукции В результирующего магнитного поля, созданного этими токами в точке О, на рисунке 2 обозначено цифрой:
Между полюсами N и S постоянного магнита находятся два тонких прямых длинных проводника 1 и 2, перпендикулярных плоскости рисунка. Сечения проводников показаны как точки. На рисунке схематически изображены линии индукции магнитного поля, созданного проводниками и магнитом. Направление линий не указано. Токи в проводниках направлены:
Между полюсами N и S постоянного магнита находятся два тонких прямых длинных проводника 1 и 2, перпендикулярных плоскости рисунка. Сечения проводников показаны как точки. На рисунке схематически изображены линии индукции магнитного поля, созданного проводниками и магнитом. Направление линий не указано. Токи в проводниках направлены:
Если плоская поверхность площадью S = 0,012 м2 расположена перпендикулярно линиям однородного магнитного поля, модуль индукции которого B = 0,40 Тл, то модуль магнитного потока ![]() через эту поверхность равен:
через эту поверхность равен:
Если плоская поверхность площадью S = 0,04 м2 расположена перпендикулярно линиям однородного магнитного поля, модуль индукции которого B = 0,20 Тл, то модуль магнитного потока ![]() через эту поверхность равен:
через эту поверхность равен:
Если плоская поверхность площадью S = 0,04 м2 расположена перпендикулярно линиям индукции однородного магнитного поля, модуль индукции которого B = 0,2 Тл, то модуль магнитного потока ![]() через эту поверхность равен:
через эту поверхность равен:
Если плоская поверхность площадью S = 0,02 м2 расположена перпендикулярно линиям индукции однородного магнитного поля, модуль индукции которого B = 0,3 Тл, то модуль магнитного потока ![]() через эту поверхность равен:
через эту поверхность равен:
Если плоская поверхность площадью S = 0,050 м2 расположена перпендикулярно линиям индукции однородного магнитного поля, модуль индукции которого B = 0,20 Тл, то модуль магнитного потока ![]() через эту поверхность равен:
через эту поверхность равен:
Если плоская поверхность площадью S = 0,030 м2 расположена перпендикулярно линиям индукции однородного магнитного поля, модуль индукции которого B = 0,50 Тл, то модуль магнитного потока ![]() через эту поверхность равен:
через эту поверхность равен:
На рисунке изображен график зависимости силы тока I в катушке индуктивности от времени t. Если индуктивность катушки L = 2,5 Гн, то собственный магнитный поток Ф, пронизывающий витки катушки, в момент времени t = 14 с равен:
На рисунке изображен график зависимости силы тока I в катушке индуктивности от времени t. Если индуктивность катушки L = 2,5 Гн, то собственный магнитный поток Ф, пронизывающий витки катушки, в момент времени t = 16 с равен:
На рисунке изображен график зависимости силы тока I в катушке индуктивности от времени t. Если индуктивность катушки L = 2,5 Гн, то собственный магнитный поток Ф, пронизывающий витки катушки, в момент времени t = 8 с равен:
На рисунке изображен график зависимости силы тока I в катушке индуктивности от времени t. Если индуктивность катушки L = 2,5 Гн, то собственный магнитный поток Ф, пронизывающий витки катушки, в момент времени t = 2 с равен:
На рисунке изображен график зависимости силы тока I в катушке индуктивности от времени t. Если индуктивность катушки L = 2,5 Гн, то собственный магнитный поток Ф, пронизывающий витки катушки, в момент времени t = 16 с равен:
Прямоугольная рамка со сторонами а = 50 мм, b = 40 мм, изготовленная из тонкой проволоки, расположена в однородном магнитном поле, линии индукции которого перпендикулярны плоскости рамки. Если в течение промежутка времени  мс модуль индукции магнитного поля равномерно уменьшился от В1 = 700 мТл до В2 = 300 мТл, то ЭДС индукции
мс модуль индукции магнитного поля равномерно уменьшился от В1 = 700 мТл до В2 = 300 мТл, то ЭДС индукции ![]() в рамке равна:
в рамке равна:
Прямоугольная рамка площадью S, изготовленная из тонкой проволоки, расположена в однородном магнитном поле, линии индукции которого перпендикулярны плоскости рамки. В течение промежутка времени  мс модуль индукции магнитного поля равномерно уменьшился от В1 = 250 мТл до В2 = 50 мТл. Если ЭДС индукции в рамке ε = 3,2 мВ, то площадь S рамки равна:
мс модуль индукции магнитного поля равномерно уменьшился от В1 = 250 мТл до В2 = 50 мТл. Если ЭДС индукции в рамке ε = 3,2 мВ, то площадь S рамки равна:
Прямоугольная рамка со сторонами а = 40 мм, b = 20 мм, изготовленная из тонкой проволоки, расположена в однородном магнитном поле, линии индукции которого перпендикулярны плоскости рамки. Модуль индукции магнитного поля равномерно уменьшился от В1 = 500 мТл до В2 = 300 мТл в течение промежутка времени ![]() Если ЭДС индукции в рамке
Если ЭДС индукции в рамке ![]() = 3,2 мВ, то промежуток времени
= 3,2 мВ, то промежуток времени ![]() равен:
равен:
На рисунке представлен график зависимости силы тока, проходящего по замкнутому проводящему контуру с постоянной индуктивностью, от времени. Интервал времени, в пределах которого значение модуля ЭДС самоиндукции ![]() максимально:
максимально:
На рисунке представлен график зависимости силы тока, проходящего по замкнутому проводящему контуру с постоянной индуктивностью, от времени. Интервал времени, в пределах которого значение модуля ЭДС самоиндукции |ε| минимально:
На рисунке представлен график зависимости силы тока, проходящего по замкнутому проводящему контуру с постоянной индуктивностью, от времени. Интервал времени, в пределах которого значение модуля ЭДС самоиндукции |ε| максимально:
Зависимость силы тока I в катушке индуктивности от времени t показана на рисунке. Для модулей ЭДС самоиндукции

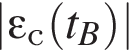 и
и 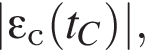 возникающей в катушке в моменты времени tA, tB и tC соответственно, справедливо соотношение:
возникающей в катушке в моменты времени tA, tB и tC соответственно, справедливо соотношение:
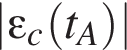 >
>  >
> 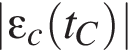
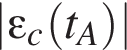 >
> 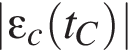 >
> 
 =
= 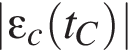 >
> 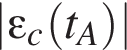
 >
> 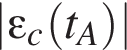 =
= 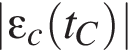
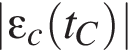 >
>  >
> 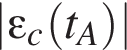
Зависимость силы тока I в катушке индуктивности от времени t показана на рисунке. Для модулей ЭДС самоиндукции

 и
и  возникающей в катушке в моменты времени tA, tB и tC соответственно, справедливо соотношение:
возникающей в катушке в моменты времени tA, tB и tC соответственно, справедливо соотношение:
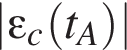 >
>  >
> 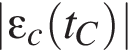
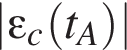 >
> 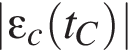 >
> 
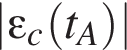 =
=  >
> 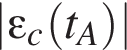
 >
> 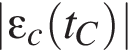 >
> 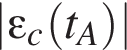
 >
> 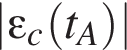 =
= 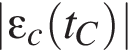
На рисунке изображён соленоид, по обмотке которого протекает постоянный ток в направлении, указанном стрелкой. Вдоль оси соленоида расположены два постоянных магнита. Строка, в которой правильно описано взаимодействие магнитов с соленоидом, обозначена цифрой:
График магнитного потока Ф через некоторую поверхность от времени t представлен на рисунке. Изменение магнитного потока ![]() за время
за время 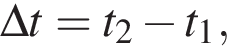 где
где  с,
с, с
с
На рисунке изображён соленоид, по обмотке которого протекает постоянный ток в направлении, указанном стрелкой. Вдоль оси соленоида расположены два постоянных магнита. Строка, в которой правильно описано взаимодействие магнитов с соленоидом, обозначена цифрой:
График магнитного потока Ф через некоторую поверхность от времени t представлен на рисунке. Изменение магнитного потока ![]() за время
за время 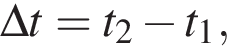 где t1 = 9 с, t2 = 11 c, равно:
где t1 = 9 с, t2 = 11 c, равно:
Квадратная проволочная рамка с длиной стороны a = 4,0 см помещена в однородное магнитное поле, модуль индукции которого B = 450 мТл, так, что линии индукции перпендикулярны плоскости рамки. Если сопротивление проволоки рамки R = 30 мОм, то при исчезновении поля через поперечное сечение проволоки рамки пройдет заряд, модуль |q| которого равен ... мКл.
Квадратная проволочная рамка с длиной стороны a = 3,0 см помещена в однородное магнитное поле, модуль индукции которого B = 620 мТл, так, что линии индукции перпендикулярны плоскости рамки. Если при исчезновении поля через поперечное сечение проволоки рамки пройдет заряд, модуль которого |q| = 18 мКл, то сопротивление R проволоки рамки равно... мОм.
Квадратная проволочная рамка с длиной стороны a = 5,0 см и сопротивлением проволоки R = 7,5 мОм помещена в однородное магнитное поле так, что линии индукции перпендикулярны плоскости рамки. Если при исчезновении поля через поперечное сечение проволоки рамки пройдет заряд, модуль которого |q| = 9,0 мКл, то модуль индукции B до исчезновения поля равен ... мТл.
Тонкое проволочное кольцо радиусом r = 4,0 см и массой m = 98,6 мг, изготовленное из проводника сопротивлением R = 0,40 Ом, находится в неоднородном магнитном поле, проекция индукции которого на ось Ox имеет вид Bx = kx, где k = 4,0 Тл/м, x — координата. В направлении оси Ox кольцу ударом сообщили скорость, модуль которой υ0 = 4,0 м/с. Если плоскость кольца во время движения была перпендикулярна оси Ox, то до остановки кольцо прошло расстояние s, равное ... см.
Тонкое проволочное кольцо радиусом r = 2,0 см и массой m = 98,6 мг, изготовленное из проводника сопротивлением R = 40 мОм, находится в неоднородном магнитном поле, проекция индукции которого на ось Ox имеет вид Bx = kx, где k = 10 Тл/м, x — координата. В направлении оси Ox кольцу ударом сообщили скорость, модуль которой υ0 = 10 м/с. Если плоскость кольца во время движения была перпендикулярна оси Ox, то до остановки кольцо прошло расстояние s, равное ... см.
Тонкое проволочное кольцо радиусом r = 3,0 см и массой m = 98,6 мг, изготовленное из проводника сопротивлением R = 81 мОм, находится в неоднородном магнитном поле, проекция индукции которого на ось Ox имеет вид Bx = kx, где k = 2,0 Тл/м, x — координата. В направлении оси Ox кольцу ударом сообщили скорость, модуль которой υ0 = 3,0 м/с. Если плоскость кольца во время движения была перпендикулярна оси Ox, то до остановки кольцо прошло расстояние s, равное ... см.
Тонкое проволочное кольцо радиусом r = 4,0 см и массой m = 98,6 мг, изготовленное из проводника сопротивлением R = 90 мОм, находится в неоднородном магнитном поле, проекция индукции которого на ось Ox имеет вид Bx = kx, где k = 2,0 Тл/м, x — координата. В направлении оси Ox кольцу ударом сообщили скорость, модуль которой υ0 = 5,0 м/с. Если плоскость кольца во время движения была перпендикулярна оси Ox, то до остановки кольцо прошло расстояние s, равное ... см.
Тонкое проволочное кольцо радиусом r = 5,0 см и массой m = 98,6 мг, изготовленное из проводника сопротивлением R = 40 мОм, находится в неоднородном магнитном поле, проекция индукции которого на ось Ox имеет вид Bx = kx, где k = 1,0 Тл/м, x — координата. В направлении оси Ox кольцу ударом сообщили скорость, модуль которой υ0 = 10 м/с. Если плоскость кольца во время движения была перпендикулярна оси Ox, то до остановки кольцо прошло расстояние s, равное ... см.
Физической величиной, измеряемой в веберах (Вб), является:
На рисунке изображен постоянный магнит. В точку A поместили небольшую магнитную стрелку, которая может свободно вращаться. Установившееся положение стрелки на рисунке обозначено цифрой:
На рисунке изображён постоянный магнит. В точку A поместили небольшую магнитную стрелку, которая может свободно вращаться. Установившееся положение стрелки на рисунке обозначено цифрой:


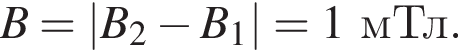
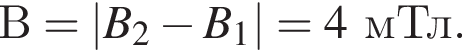
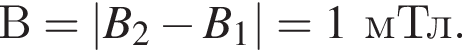
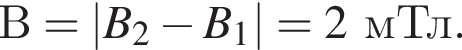
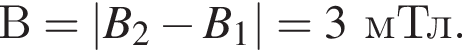





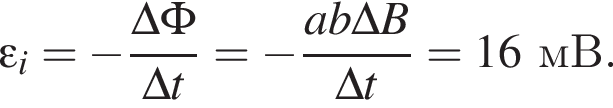
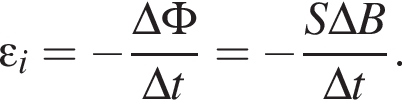
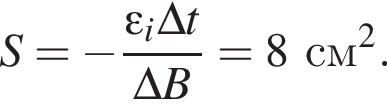
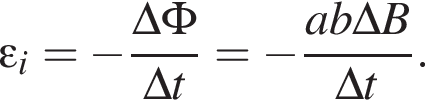
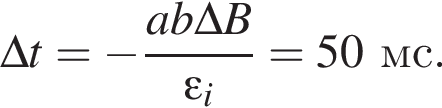
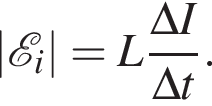
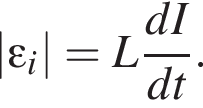
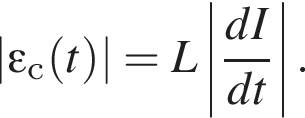
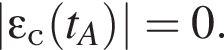 В моменты времени tB и tC модули наклона графика одинаковы, поэтому
В моменты времени tB и tC модули наклона графика одинаковы, поэтому  Таким образом,
Таким образом, 
 В моменты времени tA и tB модули наклона графика одинаковы, поэтому
В моменты времени tA и tB модули наклона графика одинаковы, поэтому  Таким образом,
Таким образом, 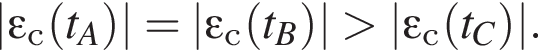
 c
c 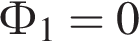 Вб,
Вб, c
c Вб
Вб Вб.
Вб. Вб,
Вб, с
с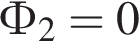 Вб.
Вб.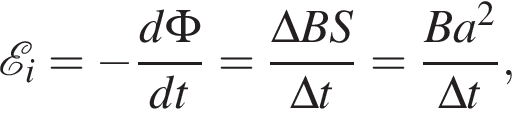
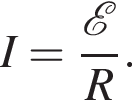
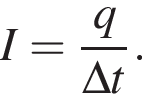
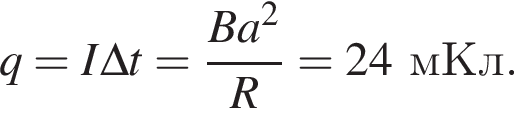
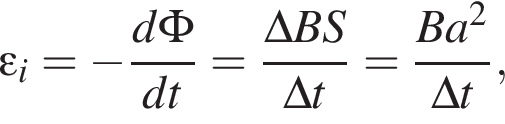
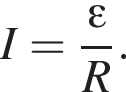
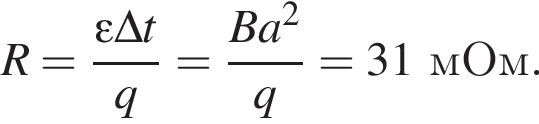
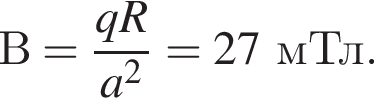
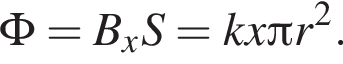 Поскольку k,
Поскольку k,